先日の練習、お疲れさまでした。今回のブログ担当のくにです。
男性6人、女性1人、それに見学者1名(女性)の8人が集まりました。
後半の自由練習時、ふじさんは三脚にiPadとかをセットして自分の動画を撮っていましたね。だんだんこういう時代になってきました。
見学者のMさんは中学で少しやって数十年?、最近遠方の息子さんから、「卓球をしなさい」とラケット(見るとちゃんとしたラバーが貼られている)が送られてきたそうです。数十年経っているのでほとんど初心者状態でしたが、息子さんの言う通り、是非続けてください。「たかさん」のように数年前は初心者でしたが、今ではベテラン達に交じってダブルスしても、遜色ない位にまで成長しました。卓球は、誰でも、いつ始めても、経験量(ラケット振った総回数)に比例して上達する「積分効果」が大きいスポーツと思います。
最近自分が考え込んでいることは、みんな経験あると思いますが、レシーブで(ラケットの角度は変えていないのに)急に強打を受けるとボールが落ちてネットにかかりやすいことです。「ボールの勢いに押される」などと言うことがありますが、その理由、仕組みをここの処ずっと考えていて、大体分かってきました。主な理由は、①ボールが速くなるとボールとラケットの反発係数が小さくなることです。(反発係数が小さくなる原因はラバー、ラケット側だけでなく、ボール側にもあります[一般にものが変形するとき内部損失が生じるため]。法政大学研究室の優れた論文ありました(論文PDFダウンロードされたし)。もし、ラケット・ラバーのメーカが強打でも反発係数があまり下がらないような製品を作ったとしても、相手のボール側の特性が支配します)(2023.11.2追記)また、②ボールが速くなるとボールとラケットの接触時間が短くなる(こちらは専門的に言うと、弾性体の非線形効果に依ります。※事象がもし線形的[線形微分方程式に従う]なら接触時間は短くも長くもならず一定のはずです。(2024.1.6追記)テニス科学の川副研究室の論文1論文2論文3参照、また小生自作の「接触時間テスター」でも実際に分かりました)(2023.11.2追記)ことも関係あると思います。それはボールを持ち上げる(擦って引っ掛ける)ラケット面平行方向の力の「力積」(力×時間)がボールが速くなるにつれて「伸び悩む」からです。
以下、自分のノートを載せます。
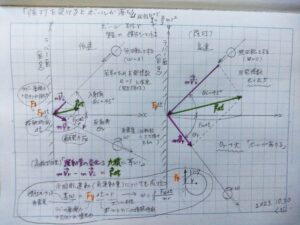
※衝突過程(入射/インパクト/反射)を単純化して図示しましたが、実際はボールの入射方向は水平に近く、ラケットは被せぎみで前方上方に動くという位置関係が多いでしょう。でも衝突過程を理解するには変わりありません。あと、ラケット面垂直方向(x軸)と平行方向(y軸)に分けて(ベクトルの成分に分けて)考えることが大事です(2023.11.2追記)
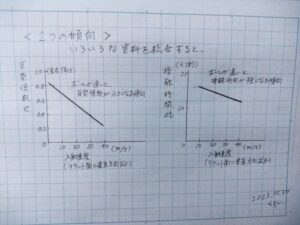
※接触時間(⊿t)は、ラバー(スポンジ)が厚い程、また柔らかい程、接触時間は全体的に長くなります。因みに、裏ソフトと表ソフトで接触時間の違いはありません。(小生も実験で確認済です~別記事)(裏ソフトの方が接触時間が長いように感じるのは、ボールの軌道が弧線で経路長が長く、初速が一緒でも相手のコートに到達するまでの時間が実際長いので、そこで錯覚が生じているのです)(2023.11.2追記)
自分、なぜこんなにまでして、物事にのめり込んでいるかというと、10年前、師匠に「へたくそ、あんた、物理出身やろ」と言われたのです。「関係ないでしょ」ととっさに返しましたが、内心今でも気になっているのです。
雇用延長も果たして、完全フリーの身になった今。かつて就職、転職の際や、会社の「目標管理カード」では「物理的センスを生かして製品開発に取り組みたい」といつも書いていましたが、これからは「物理的センスを生かして卓球に取り組みたい」と行きますww。
強打への対策、達人は強打が来たらラケット面を少し起こすとか、ラケットを上に動かすとか、ラケットを引いて相対速度を下げるとか、きっと身に付いているのでしょうね。きっと脳内に、これに特化した「ベクトル演算処理回路」が出来ているのかもしれませんねww。
自分のノートの式を総合すると、無回転のボールが固定したラケットに入射する場合の入射角θi、反射角θr(負値)、反発係数e、インパクト後のボールの回転の角速度ω(回転数に2πを掛けたもの)、ボール半径r、ラケット面垂直方向の入射速度|Vix|(正値)の関係を以下のように導けました(力積F⊿tが表に出ないようにしてみました、計算過程は省略、tanは三角関数の正接)。
tanθi + e・tanθr = (2/3)r・ω / |Vix|
(ここで、右辺のr・ωはインパクト後のボールの回転の周速に匹敵します。また、係数の2/3は卓球ボール(球殻形状)の質量と慣性モーメントの関係から出てきました)
例えば、もし反発係数が1.0(完全弾性)で、またラバーの摩擦力Fy=0(ツルッツル)と仮定すると、回転は生まれず、反射後の角速度ωは0なので、上式は、
tanθi + tanθr = 0
となり、一目瞭然、θi=-θr、θi=45°ならθr=-45°で、対称に反射し(鏡面反射)、予想通りです。
また、反発係数が0.6で、ラバーの摩擦力Fy=0(ツルッツル)と仮定すると、
tanθi + 0.6tanθr = 0
で、θi=45°なら、tan45° =1なので、
1 + 0.6tanθr = 0 ー> tanθr = -1/0.6 = -1.667 ー>
θr=arctan(-1.667) = -59.041°となります(ここでarctanはtanの逆関数)。反発係数1.0の場合と比較して約14°ボールが下に落ちます。
また、もし反発係数が0.6で、一方、ラバーの摩擦力が大きく、全く滑らず、ボールの接触点がラバー接触点に追従し、インパクト後のボール回転の周速(r・ω )がラケット面平行方向の入射速度|Viy|に一致したとすると、
tanθi + 0.6tanθr = (2/3) |Viy| / |Vix|
となり、θi=45°なら、tan45° =1、また|Viy| / |Vix| = 1なので、
1 + 0.6tanθr = 2/3 ー> tanθr = (2/3 -1)/0.6 = -0.556 ー>
θr=arctan(-0.556) = -29.074°となります。これは対称反射の-45°を逆に超え、引っ掛かりで結構ボールが持ち上がることが分かります。
(2023.11.15追記)
ついでに、上で、もし反発係数が1.0なら、
1 + tanθr = 2/3 ー> tanθr = 2/3 -1 = -0.333 ー>
θr=arctan(-0.333) = -18.435°となります。
これら4パターンを表にしました。
| 反発係数/摩擦力の4パターンの反射角θr比較
(入射角θi=45°、無回転、ラケット固定) |
摩擦なし(ツルッツル)
(回転は生まれない) |
摩擦大で、
インパクト後のボール回転周速がラケット面平行方向入射速度に等しい r・ω=|Viy| |
| 反発係数1.0 | -45° | -18.435° |
| 反発係数0.6 | -59.041° | -29.074° |
(2024.1.3追記)
いくつかの例を計算していて気が付いたのですが、(主題から逸れていきますが、)インパクト後のボール回転の周速(r・ω )とラケット面平行方向の入射速度|Viy|の関係をラバー種類別に見ると、
アンチラバー(摩擦極小)r・ω << |Viy|
表ソフトラバー(摩擦小)r・ω < |Viy|
裏ソフトラバー(摩擦大)r・ω ≒ |Viy|
更には、摩擦力だけでなくラバーの引きつれ復元力(横弾性)が大きい高弾性やテンション系の裏ソフトラバーでは、かなり r・ω >|Viy|となっているのでは!と思います(ラバー表面の横方向バネでボールが離れる直前にボールを横方向に勢いよく蹴っているイメージで、卓越した「引っ掛かり」と「回転」を生んでいる)。そしてラバーメーカはこの辺の特性を日夜、(高分子材料の配合やらを変えて)模索しているのだろうと思います。(2023.11.16追記)
上で、「かなり r・ω >|Viy|となっているのでは!」と書きましたが、本当だろうと確信してます。摩擦力(物理学では、散逸力とか非保存力と言われ、エネルギーを貯めるポテンシャルを持たない力)だけではボール回転の周速r・ω は最大でも|Viy|で、|Viy|を超えることはありません。もしそうならば、ラバーの開発なるものはとうに終わっていて、極つまらない事柄になっているでしょう。しかし現実は、たくさんのメーカがたくさんのラバーを(現在進行形で)開発していて、正に多様性の世界。それはr・ω >|Viy|の可能領域があるからといっても過言ではないでしょう。では高弾性やテンション系の裏ソフトラバーがどれくらいr・ω >|Viy|となるものだろうかというと、(測定装置がないので)自分には分かりませんが、もしr・ω = |Viy|×1.1(1割増し)だとどうなるか計算してみます。
反発係数1.0で、r・ω = |Viy|×1.1(1割増し)とすると、
tanθi + tanθr = (2/3) ×1.1×|Viy| / |Vix|
となり、θi=45°なら、tan45° =1、また|Viy| / |Vix| = 1なので、
1 + tanθr = 2/3 ×1.1 ー> tanθr = 2/3 ×1.1 -1 = -0.267 ー>
θr=arctan(-0.267) = -14.931°となります。これはr・ω = |Viy|(摩擦力だけの場合の最大値)の時より3.5°持ち上がります。
また、反発係数0.6で、r・ω = |Viy|×1.1(1割増し)とすると、
tanθi + 0.6tanθr = (2/3) ×|Viy|×1.1/ |Vix|
となり、
1 + 0.6tanθr = 2/3 ×1.1 ー> tanθr = (2/3 ×1.1 -1)/0.6 = -0.444 ー>
θr=arctan(-0.444) = -23.962°となります。これはr・ω = |Viy|(摩擦力だけの場合の最大値)の時より約5°持ち上がります。
結論としては、引きつれ復元力(横方向バネ)により、ボール回転の周速r・ω が1割増しただけで、ボールの反射角が3~5°も持ち上がることが分かりました(2024.1.19追記)
#卓球 #強打 #落ちる #反発係数 #内部損失 #接触時間 #非線形効果 #入射角 #反射角 #力積 #摩擦力 #引きつれ復元力 #回転数 #角速度 #慣性モーメント #球殻 #周速 #引っ掛かり